Genetic Programming (GP)
GP is an automated programming technique developed by John Koza
currently
at Stanford University
(More
about GP) . In 1994 I designed and built GeneCode
a GP on a 68K Mac solving the "The Santa Fe Ant Trail" as described in
John
Koza's Genetic Programming I text. The software built in
"object"
C was a GP success in that the ants could successfully traverse a 2D
trail,
but a software mistake; an example of disadvantage of object
orientation
(sub classing) without a compiler support. My program was never
ported
to PPC Mac or other system.
I would like to start another project in Java, and have a particular
stone based game in mind. The first step will be to see what is
available in Java for GP.
Link to John Koza's site
on genetic programming.
back
Santa Fe Trail
The Santa Fe Trail is a simple problem where you attempt to train
the
computer through GP to simulate an ant foraging along a broken trail of
sugar.
- The environment would be the the black pixel trail of sugar.
- The fitness test is percentage of sugar found in a fixed number
of
instructions.
- The instruction set is
- turn left 1/4 turn
- turn right 1/4 turn
- move forward
- branch forward
- is food ahead branch, else
- (I don't believe I used these but they would make good
instructions
as the ant had no state information)
- was food here branch, else
- have i been here, else
The following is output from my GeneCode program. The search for
(or
evolution of) a program was different every run because I would alter
the
size of the pool of individuals and because GP uses a randomized
starting
set. Each run is different, and no run is guaranteed to score
very
well. None of these runs exhibit perfect fitness, however
multiple
runs exhibit various approaches as you may expected in a living system.
Specifically,
both close and narrow tracking, wide tracking, and more chaotic
traversing
were exhibited.
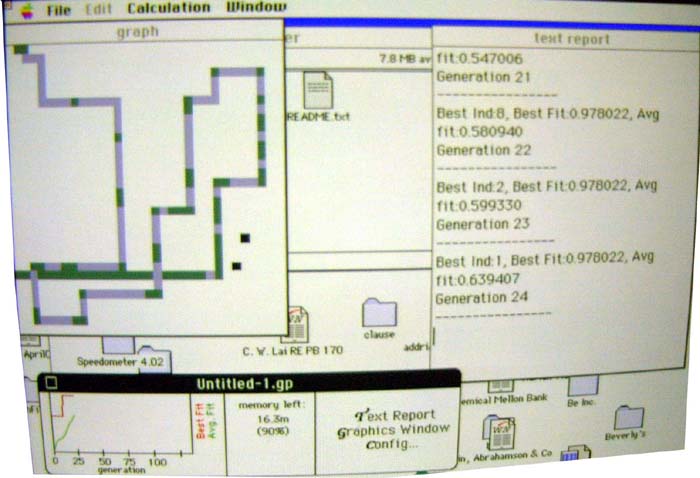
Color Key: Green indicates a space where the
ant
traveled to without finding food, blue a score - food that the ant
found,
and black food that was not discovered. The ant always beginsin
the
upper left hand corner. The graph in the bottom left is a the
fitness
measure of both the best and average of all ants in green and the best
individual
of a generation in red across the horizontal axis the generation
number.
For these runs the individual pool was between 500 and 2000
individuals.
This run took the wide but non chaotic approach, but it cannot pass a
gap
in the trail of 4 down.

This run depicts a frequent strategy, a very careful ant.
Probably
this ant looks in every direction before moving and only travels in the
direction
that last scored it some food. This approach works flawlessly
until
the end of the maze where it needs to circle around the last found food
in
widening circles to get the last two morsels. With this program I
have
no way (outside of a debugger) of reading the "instructions" generated,
but
strongly suspect that it commonly follows well because it invariably
travels
left at the last food pixel. The poor ant needs some more state
information
in its instruction set!
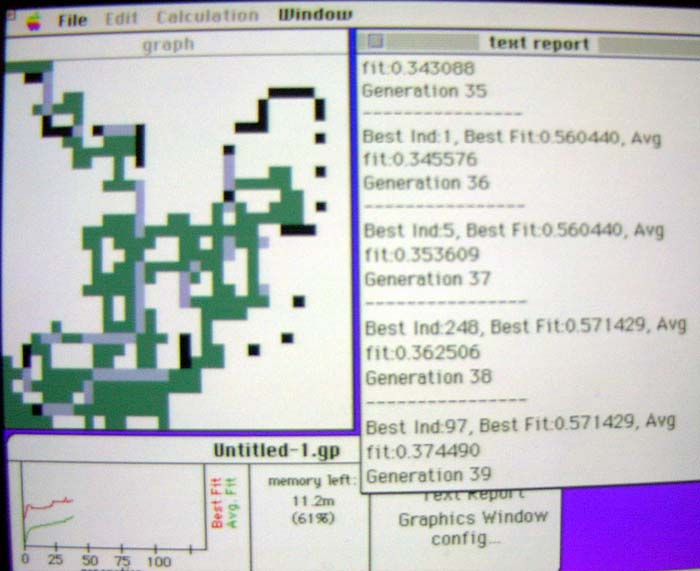
More chaotic approaches tended to be succeeded by a "good tracking"
programs.
Here's one that scores over 1/3 and has lasted to the 39th generation.
back


